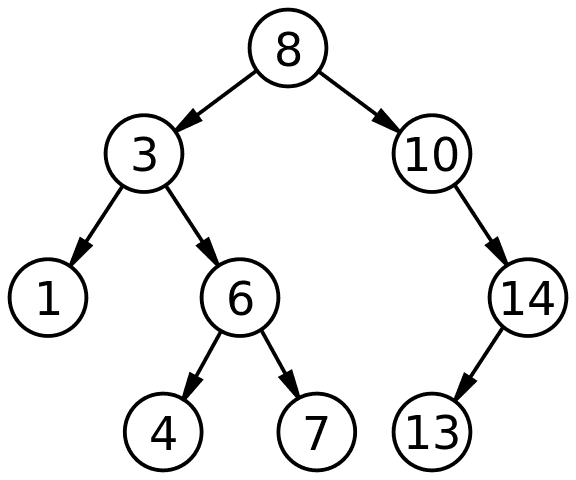
Now that you've done depth-first, let's tackle breadth-first. Breadth-first isn't recursive processing of subtrees like depth-first. Instead we want to process one layer at a time. Using the tree above, we want the resulting order to [8, 3, 10, 1, 6, 14, 4, 7, 13]. In other words, we start at the root, and slowly make our way "down" the tree.

The way we accomplish this is using our old friend, the queue. A queue is an array that the first thing you into is the first thing you get out of it (FIFO, first in first out, as opposed a stack which is first in last out, FILO.) Another way of thinking about it is that if you call dequeue on a queue, the item that has been in there the longest is the one that comes out.

What we're going to do is process the node, then add the left child to the queue and then add the right child to the queue. After that, we'll just dequeue an item off of the queue and call our function recursively on that node. You keep going until there's no items left in the queue.

Let's do the exercise! This can be solved recursively or iteratively, with the iterative result being the preferred of the two.

-> start function by adding root to the queue, queue = [8]
-> process 8, add to final array array = [8]
-> queue 3 and 10 to queue, queue = [3, 10]
-> dequeue 3, queue = [10]
-> queue 3's children, queue = [10, 1, 6]
-> add 3 to final array, array = [8, 3]
-> dequeue 10, queue = [1, 6]
-> queue 10's children, queue = [1, 6, 14]
-> add 10 to final array, array = [8, 3, 10]
-> dequeue 1, queue = [6, 14]
-> queue 1's children, nothing
-> add 1 to final array, [8, 3, 10, 1]

[etc.]

final array is [8, 3, 10, 1, 6, 14, 4, 7, 13]

So why is this useful? This is really useful if you're looking for something you know is going to be near the root of the tree or if you're looking for the "closest" (e.g. least hops) node to something. For example, if your tree represents a social network and you're looking to recommend to them who to follow, you might do a breadth-first traversal of their social contacts and recommend them people with 2 degrees of separation. Breadth-first traversal is perfect for that.

Breadth-first traversals are useful for many things and we'll be using the algorithm when we do path-finding, but the gist of when you use them is that you know the answer for what you're looking for is "closer" to the root node as opposed to far away when you would use depth-first. Again, it's all trade-offs and what you're trying to do.

Exercises

We're going to work on /specs/traversals/breadth-first.test.js. Go give that a shot.